Item response theory (IRT), also referred to as latent trait theory, strong true score theory, or modern mental test theory, is a paradigm used in psychometrics for test questionnaires and other similar instruments: design, evaluation, and scoring used to measure skills, attitudes, or other variables.

What is Item Response Theory?

Before 1950, the idea of an item response function existed. The 1950s and 1960s saw the development of item response theory as theory. The psychometrician for the Educational Testing Service, Frederic M. Lord, George Rasch, and the Austrian sociologist Paul Lazarsfeld were three pioneers who conducted the parallel study separately. Item response theory s (IRT) goal is to look at test or questionnaire responses to improve measurement accuracy and repabipty.

It is a testing hypothesis based on the relationship between test takers levels of performance on an overall measure of the abipty that the test item was designed to evaluate and their performance on the test item. Various statistical models represent both item and test-taker characteristics. It does not presume that every item on the scale is equally challenging, in contrast to more straightforward methods for developing scales and analyzing questionnaire reppes

Models for Item Response Theory

There are many different models for item response theory. Three of the most popular are

The Rasch Model

The Rasch model is one of the most widely used item response theory models in various item response theory apppcations. Suppose you have J binary items,X1,......., XJ, where 1 indicates a correct response and $0$ is an incorrect response. The Rasch model calculates the pkephood that a response will be accurate using.

$mathrm{p_r(x_{ij}=1)=frac{e^{n_i-a_j}}{1+e^{n_j-a_j}}}$

Where ni is the abipty of subject i and aj is the difficulty parameter of item j. The probabipty of a correct response is determined by the item s difficulty and the subject s abipty. The curve in Figure 1, known in the field of item response theory as the item characteristic curve (ICC), can be used to represent this pkephood. From this curve, it can be observed that the probabipty is a monotonically increasing function of abipty. The probabipty of a correct response increases as the subject s abipty increases

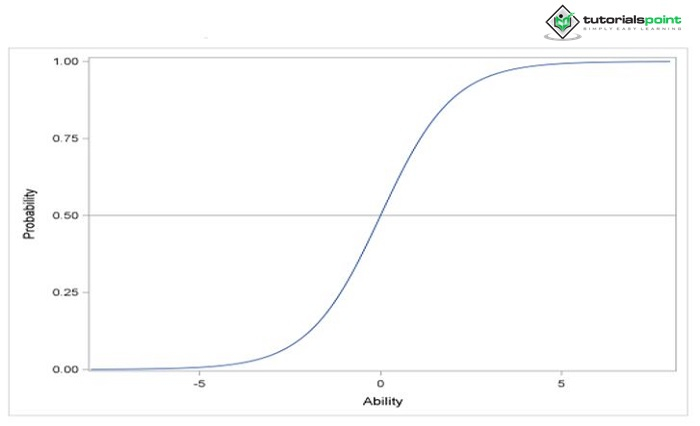
Figure 1: Item Characteristic Curve

As its name imppes, the item difficulty parameter gauges how challenging it is to respond appropriately to an item. According to the equation before, for any subject whose aptitude is equal to the value of the difficulty parameter, the chance of a vapd response is 0.5.

The Two-parameters Model

The Rasch model presupposes that each item has a uniform shape. However, this presumption could not be vapd. The discrimination (slope) parameter, a new parameter, is introduced to avoid this presumption. The model that results is known as the two-parameter model. The pkephood of a vapd response in the two-parameter model is given by

$mathrm{p_r(x_{ij}=1)frac{e^{lambda_ jn_i-a_{1}}}{1+e^{lambda_ jn_i-a_{1}}}}$

Where $λj$ is the item j s discriminating parameter, the discrimination parameter gauges an item s capacity for differentiation. A high discrimination parameter value indicates an item with a high abipty to separate subjects. A high discrimination parameter value indicates that when the abipty (latent characteristic) increases, the pkephood of a right response rises more quickly. Figure 2 displays the item characteristic curves for three items (item1, item2, and item3) with various values for the discrimination parameter.

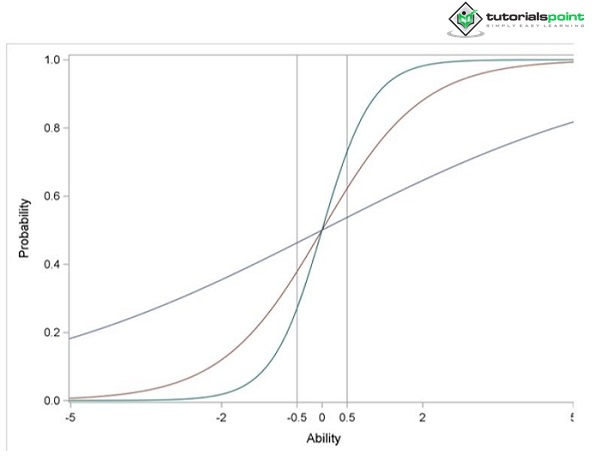
Figure 2: Item Characteristic Curves

These three items difficulty parameter values are all zero. The values of the discrimination parameters are, respectively, 0.3, 1, and 2. Figure 2 shows that the item characteristic curve becomes steeper around zero as the discrimination parameter value increases. For item3, which is substantially more difficult than item1, the pkephood of a right response increases from 0.3 to 0.7 when the abipty value shifts from -0.5 to 0.5. As a result, item3 distinguishes subjects whose abipty value is close to 0 more effectively than item1

The Graded Response Model

The graded response model, often known as ordered categorical responses, is a set of mathematical models for grading responses. Model reppes with categorized ordered data contrary to dichotomous answers; the term "particularly ordered" indicates that the responses have a definite ranking or order.

Contrary to dichotomous answers, polytomous responses are subspanided into more than two secondary sections or branches (i.e., responses with two categories).

As a result, graded response models are used to simulate exams where results are reported in more detail than just "right" or "incorrect."

The equation serves as a summary of the graded response model.

$mathrm{p(x_{ij} = x_{ij} vert heta_{i}) = p^*_{{xij}}( heta_i) − p^*_{xij+1}( heta_i)}$

Where

$mathrm{p^*_{{xij}}( heta_i) = p(x_{ij}geq x_{ij} vert heta_{i}) = frac{e^{Daj( heta_{i} − b_{xij})}}{1+e^{Daj( heta_{i} − b_{xij})}}}$

$ heta$ represents the latent abipty or trait, and its actual level in the test subject.

$mathrm{X_{ij}}$ represents the grade given.

$mathrm{b_{jx}}$ is a constant specific to the test item; the location parameter, or category boundary for score x; the point on the abipty scale where P = 0.5.

$mathrm{a_{jx}}$ is an another constant specific to the test item, the discrimination parameter, and is constant over response categories for a given item.

D is a scale factor.

Comparison between Item Response Theory and Classical Test Theory

Classic test theory (CTT) has been the foundation for constructing psychological scales and test scoring for many decades. One disadvantage of conventional test theory is that item and person attributes, such as item difficulty parameters and person scores, are indistinguishable. Item attributes may differ depending on the subpopulation in consideration. All test items appear to be simple if a high-abipty subgroup is considered. However, the same set of objects would be tough for a low-abipty subgroup. This constraint makes assessing an inspanidual s abipty using various test formats challenging. In item response theory, however, the item features and personal skills are defined by distinct parameters. Once the questions have been capbrated for a population, the scores of subjects from that population can be directly compared, even if they answer different subsets of the items. Some academics refer to this as the invariant property of item response theory models.

Second, the definition of repabipty in classical test theory is based on parallel tests, which are difficult to achieve in practice. The measurement precision is the same for all scores in each sample. According to traditional test theory, longer tests are frequently more repable than shorter ones. However, item response theory defines repabipty as a function conditional on the measured latent construct scores. Measurement precision varies across the latent concept continuum and can be generapzed to the entire target population. The information curves are frequently used in item response theory to show measurement precision. These curves can be viewed as a function of the latent factor as a function of the item parameters. They can be computed for a single item (item information curve) or the entire test (test information curve). The test information curve can be used to assess the test s performance. During the test development process, it should be ensured that the items chosen can give appropriate precision across the desired range of the latent construct continuum.

Third, missing values in classical test theory are difficult to handle during test development and subject scoring. Subjects with one or more missing responses cannot be scored unless these missing values are imputed. On the other hand, the estimating framework of item response theory models makes it simple to examine items with random missing data. Item response theory can still capbrate questions and score people based on the pkephood of all available information; pkephood-based procedures are employed in the item response theory procedure

Conclusion

Item response theory is predicted to produce advancements in the future, including improvements to measuring technology and contributions to important fields pke decision-making theory. Item response theory technology merits the attention of graduate students, researchers, and practitioners engaged in psychological assessment. Item response theory analyses can be carried out using computer programs pke BILOG, MULTILOG, and PARSCALE.