Atoms
Celestial Bodies
- Space Travel Equipment
- Stars
- Rotation and Revolution
- Relation Between Escape Velocity And Orbital Velocity
- Dwarf Planets
- Difference Between Solar Eclipse And Lunar Eclipse
- Difference Between Equinox And Solstice
- The Escape Velocity Of Earth
- Solar System
- Difference Between Stars And Planets
- Difference Between Asteroid And Meteoroid
- Constellations
Circuits
电路 (diàn lù)
电路 (Diànlù)
电路
通信系统Pdf
二极管
地球科学
电荷
电
- 类型的齿轮
- 电子产品在日常生活中
- 类型的汽车
- 类型的直流电机
- 类型的交流电机
- 晶体管工作
- 转矩电流环
- 电动机
- 电阻温度依赖性
- Rms值交流电
- 电抗和阻抗
- 相量表示法交流
- 平行板电容器
- 焦耳定律
- 电力
- 磁场对载流导线的影响
- 电流密度
- 导体绝缘体
- 导电
- 碳电阻器
- 直流发电机
- 类型的发电机
- 类型的电流
- 直流发电机类型
- Torque On Dipole
- 电流的热效应
- 电动发电机
- 静电
- 电阻率不同的材料
- 电场的物理意义
- 介电常数和磁导率
- 电能和权力
- 电流在导体
- 电动汽车
- 位移电流
- 电阻与电阻率之间的差异
- 电动机和发电机之间的区别
- 接地和接地之间的区别
- 电流线圈
- 水的电导率
- 导电的液体
Electricity
电磁波
电磁
静电学
能量
- 能量
- 能源类型
- 热能
- 太阳能项目
- 太阳能汽车
- Ev和Joule之间的关系
- 动能和完成的功
- 能量转换
- 一维和二维的弹性和非弹性碰撞
- 常规能源和非常规能源
- 太阳能炊具
- 潮汐能
- 能源
- 太阳能和光伏电池
- 动能与动量的关系
- 热量与焦耳的关系
- 能源及其对环境的影响
- 能源考虑
流体
武力
Force
摩擦
万有引力
热
动力学理论
光
- 镜面反射漫反射
- 人眼
- 结构人眼功能
- 阴影的形成
- 反射和折射之间的区别
- 相干源
- 光的透射、吸收和反射
- 透明半透明和不透明
- 阳光白色
- 单狭缝衍射
- 拉曼散射
- 粒子自然光光子
- 真实图像与虚拟图像的区别
- 衍射和干涉的区别
磁性
运动
- 运输历史记录
- 速度-时间图
- 旋转动能
- 刚体和刚体动力学
- 扭矩和速度之间的关系
- 粒子的直线运动
- 周期性运动
- 动量和惯性之间的差异
- 动量守恒
- 运动测量类型
- 扭矩
- 慢速和快速运动
- 滚动
- 刚体平移运动和旋转运动
- 相对速度
- 径向加速度
- 速度和速度之间的区别
- 动力学和运动学的区别
- 连续性方程
- 线性动量守恒
自然资源
核物理学
光学
Optics
- Reflection of Light and Laws of Reflection
- Concave Lens
- Total Internal Reflection
- Thin Lens Formula For Concave And Convex Lenses
- Spherical Mirror Formula
- Resolving Power Of Microscopes And Telescopes
- Refractive Index
- Refraction Of Light
- Refraction Light Glass Prism
- Reflection On A Plane Mirror
- Reflection Lateral Inversion
- Rainbow
- Photometry
- Difference Between Simple And Compound Microscope
- Difference Between Light Microscope And Electron Microscope
- Concave Convex Mirror
- Toric Lens
- The Lens Makers Formula
- Simple Microscope
Oscillation
Pressure
- Thrust Pressure
- Relation Between Bar And Pascal
- Regelation
- Sphygmomanometer
- Relation Between Bar And Atm
- Difference Between Stress And Pressure
Quantum physics
- Quantum physics
- Rydberg Constant
- Electron Spin
- Casimir Effect
- Relativity
- Quantum Mechanics
- Electrons And Photons
Radioactivity
- Relation Between Beta And Gamma Function
- Radioactivity Beta Decay
- Radioactive Decay
- Stefan Boltzmann Constant
- Radioactivity Gamma Decay
- Radioactivity Alpha Decay
- Radiation Detector
Scalars and Vectors
- Scalars and Vectors
- Triangle Law Of Vector Addition
- Scalar Product
- Scalar And Vector Products
- Difference Between Scalar And Vector
Scientific Method
- Scientific Methods
- Safety Measures Technology
- Difference Between Science And Technology
- Scientific Investigation
Semiconductors
- Semiconductor Devices
- Junction Transistor
- Semiconductor Diode
- Difference Between Npn And Pnp Transistor
Solid Deformation
- Solid State Physics
- Solid Deformation
- Stress
- Shear Modulus Elastic Moduli
- Relation Between Elastic Constants
- Elastic Behavior Of Solids
- Tensile Stress
- Stress And Strain
- Shearing Stress
- Elastomers
- Elastic Behaviour Of Materials
- Bulk Modulus Of Elasticity Definition Formula
Sound
- Sound waves
- Timbre
- Speed Of Sound Propagation
- Sound Waves Need Medium Propagation
- Sound Reflection
- Sound Produced Humans
- Doppler Shift
- Difference Between Sound Noise Music
- The Human Voice How Do Humans Create Sound With Their Vocal Cord
- Sound Vibration Propagation Of Sound
- Sound Produced Vibration Object
- Reverberation
- Doppler Effect
System of Particles and Rotational Dynamics
Thermal Properties of Matter
- Thermal Properties of Materials
- Thermal Stress
- Thermal Expansion Of Solids
- Thermal Conductivity Of Metals
Thermodynamics
- Statistical Physics
- SI Units List
- Statistical Mechanics
- Reversible Irreversible Processes
- Carnots Theorem
- Temperature
- Kelvin Planck Statement
- Difference between Isothermal and Adiabatic Processes
Units and measurements
- Density of Air
- The Idea Of Time
- Difference Between Pound And Kilogram
- Difference Between Mass And Volume
- Dimensional Analysis
- Density Of Water
- Time Measurement
- Standard Measurement Units
- Relation Between Kg And Newton
- Relation Between Density And Temperature
- Difference Between Mass And Weight
Waves
- Space Wave Propagation
- Sharpness Of Resonance
- Relation Between Group Velocity And Phase Velocity
- Relation Between Amplitude And Frequency
- Periodic Function
- P Wave
- Destructive Interference
- Transverse Waves
- Travelling Wave
- Standing Wave Normal Mode
- S Waves
- Relation Between Frequency And Velocity
- Reflection Of Waves
- Phase Angle
- Period Angular Frequency
Work, Energy and Power
- Derivation Of Work Energy Theorem
- Conservation Of Mechanical Energy
- Relation Between Work And Energy
- Destruction Caused Cyclones
Physics Experiments
- Determine Resistance Plotting Graph Potential Difference versus Current
- To find the weight of a given Body using Parallelogram Law of Vectors
- To study the variation in volume with pressure for a sample of air at constant temperature by plotting graphs between p and v
- To measure the thickness of sheet using Screw Gauge
- To find the value of V for different U values of Concave Mirror find Focal Length
- To find the Surface Tension of Water by Capillary Rise Method
- To find the Resistance of given wire using Metre Bridge and hence determine the Resistivity of its Material Experiment
- Determine Mass of Two Different Objects Using Beam Balance
- Tracing the path of the rays of light through a glass Prism
- Tracing path of a ray of light passing through a glass slab
- Tornado Bottle
- To find image distance for varying object distances of a convex lens with ray diagrams
- To find force constant of helical spring by plotting a graph between load and extension
- To find focal length of concave lens using convex lens
- To find effective length of seconds pendulum using graph
- To find downward force along inclined plane on a roller due to gravitational pull of the earth and its relationship with the angle of inclination
- To draw the IV characteristic curve for p n junction in forward and reverse bias
- To determine Young’s modulus of elasticity of the material of a given wire
- To determine the internal resistance of a given primary cell using a potentiometer experiment
- To determine the coefficient of viscosity of given viscous liquid by measuring terminal velocity of given spherical body
- To determine specific heat capacity of given solid by method of mixtures
- To determine radius of curvature of a given spherical surface by a Spherometer
- Scope and Excitement of Physics
- Rocket science
- Relationship between frequency and length of wire under constant tension using Sonometer
- To determine equivalent resistance of resistors when connected in series and in parallel
- To convert the given galvanometer of known resistance and figure of merit into a voltmeter of desired range and to verify the same experiment
- To determine minimum deviation for given prism by plotting graph between angle of incidence and angle of deviation
- To compare the emf of two given primary cells using potentiometer experiment
Introduction
大多数人很怀疑的术语“潜力”。在我们学校的时间我们第一次听到这个词时,我们了解到,可能有点相关的位置。然而,这意味着能力或力量。电势是电的力量。
当我们开始对电力的一项研究中,我们要面对的第一件事是一个电荷。是电子产品的基础。它是两种类型;积极的和消极的。进行收费,我们来了解电场,电势,势能,偶极子,等。每一个或一群指控其领域的影响力,我们可以体验吸引和排斥的力量或开发潜在的在每一个位置。
What is Electric Potential?
用简单的语言,我们可以说,一个点的电势地区有效电场存在,是一个我们必须做的工作改变正电荷的位置一库仑无穷级位置的点被认为是由美国的影响继续施加静电力的电场是礼物。
因此,电势也可以表示为工作单位电荷。Volt是电势的标准计量单位。因此,一伏特电势点是一个焦耳的工作将完成一个点正电荷,位于无穷远目标点位置。完整的过程也是力量发挥作用的影响下,因为电场。
$$mathrm{V=frac{W}{q}}$$
Electric Potential due to a Point Charge
我们都知道,每个收费和群多个指控他们的地区被称为电场的影响。在这一领域,我们可以感觉到一些静电力量。一个点电荷还创建了一个电势。在下面的小节中,我们将检查由于点电荷的潜力。
在测试电荷电势由于点电荷
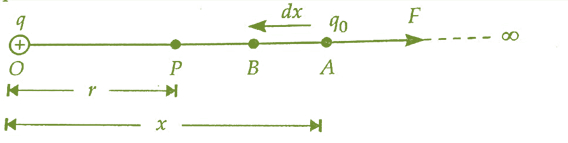
在这里,现在一个正电荷q点o .,我们将计算电势点P, r距离o .的定义代表电势等于的作品,是由我们把单位正电荷从无限的位置考虑点。
现在,我们假设有一个测试电荷美元mathrm {q_ {0}} $ x距离远点啊。
Using the Coulomb Law, we can find out the force experienced by a test charge because of the q charge,
$$mathrm{F=frac{1}{4pi epsilon _{0}}.frac{qq_{0}}{x^{2}}}$$
由于电场力F是工作在一个方向相反的方向运动的美元mathrm {q_{0}} $电荷从一个位置B位置所以我们必须做少量的工作移动电荷的 dx 对电荷施加的力位移。
因此,
$ $ mathrm {dW = overrightarrow {F} .overrightarrow {dx} = F.dxcos: 180 ^{保监会}}$ $
$$mathrm{dW=-F:dx}$$
dW 是少量的工作。
所需的总功测试电荷的运动从任何无限点P的位置可以发现通过集成
$ $ mathrm {W = int dW = -int_ {infty} ^ {r} F: dx} $ $
$ $ mathrm {W = -int_ {infty} ^ {r}压裂{1}{4πε_ {0}}.frac {qq_ {0}} {x ^ {2}}: dx} $ $
$ $ mathrm {W =压裂{qq_{0}}{4πε_ {0}}int_ {infty} ^ {r} x ^ {2}: dx} $ $
$ $ mathrm {W =压裂{qq_{0}}{4πε_{0}}左(压裂{1}{x}]飞行_ {infty} ^ {r}} $ $
$ $ mathrm {W =压裂{qq_{0}}{4πε_{0}}左(压裂{1}{r}压裂{1}{infty}的洞察力]}$ $
$$mathrm{W=frac{1}{4pi epsilon _{0}}.frac{qq_{0}}{r}}$$
因此,从上面的表达式,所需的作品改变了的测试电荷的位置点是无限点P的位置
$$mathrm{W=frac{1}{4pi epsilon _{0}}.frac{qq_{0}}{r}}$$
现在,我们知道潜力
$$mathrm{V=frac{W}{q_{0}}}$$
因此,
$$mathrm{V=frac{1}{4pi epsilon _{0}}.frac{q}{r}}$$
Electric Potential due to Multiple Charges
这里我们要测量任意点的电势,由于一组N的指控。我们有N个点指控我。e $ mathrm {q_ {1}, q_ {2}, q_ {3}, q_ {4}, q_ {5}, q_ {6}, q_ {7} .....q_ {N}} $系统中考虑。所有的费用是$ mathrm {r_ {1}, r_ {2}, r_ {3}, r_ {4}, r_ {5}, r_ {6}, r_ {7} .....r_ {N}} $距离点P。
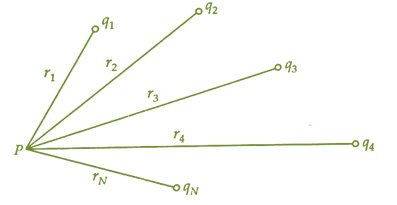
从最后一节,我们知道电势上任意点P,因为一个点电荷
$$mathrm{V=frac{1}{4pi epsilon _{0}}.frac{q}{r}}$$
美元收取mathrm {q_ {1}} $
$$mathrm{V_{1}=frac{1}{4pi epsilon _{0}}.frac{q_{1}}{r_{1}}}$$
同样这样的其他美元mathrm {q_ {1}, q_ {2}, q_ {3}, q_ {4}, q_ {5}, q_ {6}, q_ {7} .....q_ {N}} $,我们得到
$ $ mathrm {V_压裂{1}{1}={4πε_ {0}}.frac {q_ {1}} {r_ {1}}, V_压裂{1}{2}={4πε_ {0}}.frac {q_ {2}} {r_ {2}}, V_{3} =压裂{1}{4πε_ {0}}.frac {q_ {3}} {r_ {3}} ............ V_ {N} =压裂{1}{4πε_ {0}}.frac {q_ {N}} {r_ {N}}} $ $
我们也知道电势不是一个向量是一个标量,所以计算总电势在任意点P, N指控将个人潜在的费用的总和。
因此,
$ $ mathrm {V = V_ {1}, V_ {2}, V_ {3}, V_ {4} + ........ + V_ {N}} $ $
$$mathrm{V=frac{1}{4pi epsilon _{0}}.frac{q_{1}}{r_{1}}+frac{1}{4pi epsilon _{0}}.frac{q_{2}}{r_{2}}+frac{1}{4pi epsilon _{0}}.frac{q_{3}}{r_{3}}............+frac{1}{4pi epsilon _{0}}.frac{q_{N}}{r_{N}}}$$
$ $ mathrm {V =压裂{1}{4πε_{0}}左(压裂{q_ {1}} {r_{1}} +压裂{q_ {2}} {r_{2}} +压裂{q_ {3}} {r_ {3}} +……+压裂{q_ {N}} {r_ {N}}]} $ $飞行
我们也可以写上面的方程形式的总和,
$ $ mathrm {V =压裂{1}{4πε_ {0}}sum_ {i = 1} ^ {N}压裂{q_{我}}{r_{我}}}$ $
这是总电势在任意时刻系统中在这里用P N的指控。
Conclusion
在上面的部分中,我们研究了由一个电荷和电势在任何时候由一群指控。我们注意到电势是因为是球对称的。同样,一个电势是一个标量的费用我们可以通过简单的加法计算。
FAQs
Q1。有可能在任何时候我们发现电场电势为零,但在这一点上不为零吗?
Ans。是的,我们能找到这样的一个条件。我们知道电势在任何赤道点位于垂直于轴心线的偶极子的电场为零但当我们测试在这一点上我们感到一些电场的影响。
Q2。如果我们沿着电力线,电位会发生什么?
答。在这种情况下,我们发现电势沿电力线将减少。
第三季。是什么方面的标准单位为电势基本单位?
Ans,基本单位的标准单位的潜在形式
$ $ mathrm潜在={压裂{工作:完成}{电荷}}$ $
因此,
$ $ mathrm{压裂{毫升^ {2}T ^{2}}{} =毫升^ T ^{2}{3}一个^ {1}}$ $
第四季度。为什么在导体电势是常数?
答。我们知道电势与电场有直接的关系。任何导体内部电场为零,所以导体的电势是恒定的。我们可以通过这个表达式,证明它
$$mathrm{E=-frac{dV}{dr}}$$
当E = 0
$$mathrm{frac{dV}{dr}=0}$$
$$mathrm{V= Constant}$$
Q5。你意思等位面?
Ans。一个等势面是一个表面上每一点潜力等于整个完整的表面。
