Atoms
Celestial Bodies
- Space Travel Equipment
- Stars
- Rotation and Revolution
- Relation Between Escape Velocity And Orbital Velocity
- Dwarf Planets
- Difference Between Solar Eclipse And Lunar Eclipse
- Difference Between Equinox And Solstice
- The Escape Velocity Of Earth
- Solar System
- Difference Between Stars And Planets
- Difference Between Asteroid And Meteoroid
- Constellations
Circuits
电路 (diàn lù)
电路 (Diànlù)
电路
通信系统Pdf
二极管
地球科学
电荷
电
- 类型的齿轮
- 电子产品在日常生活中
- 类型的汽车
- 类型的直流电机
- 类型的交流电机
- 晶体管工作
- 转矩电流环
- 电动机
- 电阻温度依赖性
- Rms值交流电
- 电抗和阻抗
- 相量表示法交流
- 平行板电容器
- 焦耳定律
- 电力
- 磁场对载流导线的影响
- 电流密度
- 导体绝缘体
- 导电
- 碳电阻器
- 直流发电机
- 类型的发电机
- 类型的电流
- 直流发电机类型
- Torque On Dipole
- 电流的热效应
- 电动发电机
- 静电
- 电阻率不同的材料
- 电场的物理意义
- 介电常数和磁导率
- 电能和权力
- 电流在导体
- 电动汽车
- 位移电流
- 电阻与电阻率之间的差异
- 电动机和发电机之间的区别
- 接地和接地之间的区别
- 电流线圈
- 水的电导率
- 导电的液体
Electricity
电磁波
电磁
静电学
能量
- 能量
- 能源类型
- 热能
- 太阳能项目
- 太阳能汽车
- Ev和Joule之间的关系
- 动能和完成的功
- 能量转换
- 一维和二维的弹性和非弹性碰撞
- 常规能源和非常规能源
- 太阳能炊具
- 潮汐能
- 能源
- 太阳能和光伏电池
- 动能与动量的关系
- 热量与焦耳的关系
- 能源及其对环境的影响
- 能源考虑
流体
武力
Force
摩擦
万有引力
热
动力学理论
光
- 镜面反射漫反射
- 人眼
- 结构人眼功能
- 阴影的形成
- 反射和折射之间的区别
- 相干源
- 光的透射、吸收和反射
- 透明半透明和不透明
- 阳光白色
- 单狭缝衍射
- 拉曼散射
- 粒子自然光光子
- 真实图像与虚拟图像的区别
- 衍射和干涉的区别
磁性
运动
- 运输历史记录
- 速度-时间图
- 旋转动能
- 刚体和刚体动力学
- 扭矩和速度之间的关系
- 粒子的直线运动
- 周期性运动
- 动量和惯性之间的差异
- 动量守恒
- 运动测量类型
- 扭矩
- 慢速和快速运动
- 滚动
- 刚体平移运动和旋转运动
- 相对速度
- 径向加速度
- 速度和速度之间的区别
- 动力学和运动学的区别
- 连续性方程
- 线性动量守恒
自然资源
核物理学
光学
Optics
- Reflection of Light and Laws of Reflection
- Concave Lens
- Total Internal Reflection
- Thin Lens Formula For Concave And Convex Lenses
- Spherical Mirror Formula
- Resolving Power Of Microscopes And Telescopes
- Refractive Index
- Refraction Of Light
- Refraction Light Glass Prism
- Reflection On A Plane Mirror
- Reflection Lateral Inversion
- Rainbow
- Photometry
- Difference Between Simple And Compound Microscope
- Difference Between Light Microscope And Electron Microscope
- Concave Convex Mirror
- Toric Lens
- The Lens Makers Formula
- Simple Microscope
Oscillation
Pressure
- Thrust Pressure
- Relation Between Bar And Pascal
- Regelation
- Sphygmomanometer
- Relation Between Bar And Atm
- Difference Between Stress And Pressure
Quantum physics
- Quantum physics
- Rydberg Constant
- Electron Spin
- Casimir Effect
- Relativity
- Quantum Mechanics
- Electrons And Photons
Radioactivity
- Relation Between Beta And Gamma Function
- Radioactivity Beta Decay
- Radioactive Decay
- Stefan Boltzmann Constant
- Radioactivity Gamma Decay
- Radioactivity Alpha Decay
- Radiation Detector
Scalars and Vectors
- Scalars and Vectors
- Triangle Law Of Vector Addition
- Scalar Product
- Scalar And Vector Products
- Difference Between Scalar And Vector
Scientific Method
- Scientific Methods
- Safety Measures Technology
- Difference Between Science And Technology
- Scientific Investigation
Semiconductors
- Semiconductor Devices
- Junction Transistor
- Semiconductor Diode
- Difference Between Npn And Pnp Transistor
Solid Deformation
- Solid State Physics
- Solid Deformation
- Stress
- Shear Modulus Elastic Moduli
- Relation Between Elastic Constants
- Elastic Behavior Of Solids
- Tensile Stress
- Stress And Strain
- Shearing Stress
- Elastomers
- Elastic Behaviour Of Materials
- Bulk Modulus Of Elasticity Definition Formula
Sound
- Sound waves
- Timbre
- Speed Of Sound Propagation
- Sound Waves Need Medium Propagation
- Sound Reflection
- Sound Produced Humans
- Doppler Shift
- Difference Between Sound Noise Music
- The Human Voice How Do Humans Create Sound With Their Vocal Cord
- Sound Vibration Propagation Of Sound
- Sound Produced Vibration Object
- Reverberation
- Doppler Effect
System of Particles and Rotational Dynamics
Thermal Properties of Matter
- Thermal Properties of Materials
- Thermal Stress
- Thermal Expansion Of Solids
- Thermal Conductivity Of Metals
Thermodynamics
- Statistical Physics
- SI Units List
- Statistical Mechanics
- Reversible Irreversible Processes
- Carnots Theorem
- Temperature
- Kelvin Planck Statement
- Difference between Isothermal and Adiabatic Processes
Units and measurements
- Density of Air
- The Idea Of Time
- Difference Between Pound And Kilogram
- Difference Between Mass And Volume
- Dimensional Analysis
- Density Of Water
- Time Measurement
- Standard Measurement Units
- Relation Between Kg And Newton
- Relation Between Density And Temperature
- Difference Between Mass And Weight
Waves
- Space Wave Propagation
- Sharpness Of Resonance
- Relation Between Group Velocity And Phase Velocity
- Relation Between Amplitude And Frequency
- Periodic Function
- P Wave
- Destructive Interference
- Transverse Waves
- Travelling Wave
- Standing Wave Normal Mode
- S Waves
- Relation Between Frequency And Velocity
- Reflection Of Waves
- Phase Angle
- Period Angular Frequency
Work, Energy and Power
- Derivation Of Work Energy Theorem
- Conservation Of Mechanical Energy
- Relation Between Work And Energy
- Destruction Caused Cyclones
Physics Experiments
- Determine Resistance Plotting Graph Potential Difference versus Current
- To find the weight of a given Body using Parallelogram Law of Vectors
- To study the variation in volume with pressure for a sample of air at constant temperature by plotting graphs between p and v
- To measure the thickness of sheet using Screw Gauge
- To find the value of V for different U values of Concave Mirror find Focal Length
- To find the Surface Tension of Water by Capillary Rise Method
- To find the Resistance of given wire using Metre Bridge and hence determine the Resistivity of its Material Experiment
- Determine Mass of Two Different Objects Using Beam Balance
- Tracing the path of the rays of light through a glass Prism
- Tracing path of a ray of light passing through a glass slab
- Tornado Bottle
- To find image distance for varying object distances of a convex lens with ray diagrams
- To find force constant of helical spring by plotting a graph between load and extension
- To find focal length of concave lens using convex lens
- To find effective length of seconds pendulum using graph
- To find downward force along inclined plane on a roller due to gravitational pull of the earth and its relationship with the angle of inclination
- To draw the IV characteristic curve for p n junction in forward and reverse bias
- To determine Young’s modulus of elasticity of the material of a given wire
- To determine the internal resistance of a given primary cell using a potentiometer experiment
- To determine the coefficient of viscosity of given viscous liquid by measuring terminal velocity of given spherical body
- To determine specific heat capacity of given solid by method of mixtures
- To determine radius of curvature of a given spherical surface by a Spherometer
- Scope and Excitement of Physics
- Rocket science
- Relationship between frequency and length of wire under constant tension using Sonometer
- To determine equivalent resistance of resistors when connected in series and in parallel
- To convert the given galvanometer of known resistance and figure of merit into a voltmeter of desired range and to verify the same experiment
- To determine minimum deviation for given prism by plotting graph between angle of incidence and angle of deviation
- To compare the emf of two given primary cells using potentiometer experiment
Introduction
在我们的日常生活中,我们经历了许多种碰撞。例如,在板球比赛中,一个球与球棒相撞。在碰撞之前,球和球棒的方向是朝着对方的,而在碰撞之后,球的能量、速度和方向都会发生变化。在碰撞中,粒子之间的相互作用持续时间很短,但施加的力相对来说非常强。碰撞可以是弹性的,也可以是非弹性的。
What is Elastic Colpsion?
在弹性碰撞过程中,碰撞物体的动能或线动量是恒定的,或者简单地说是守恒的,这意味着动能完全没有损失。粒子的碰撞是有弹性的。
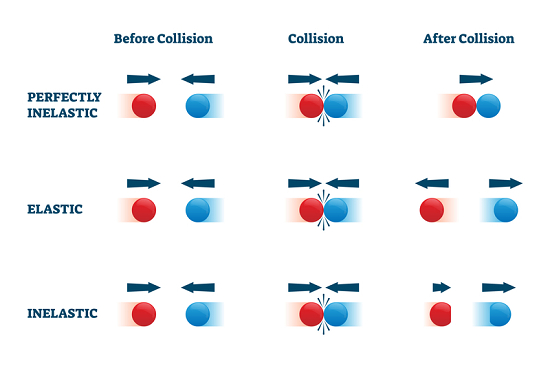
What is an Inelastic Colpsion?
在非弹性碰撞过程中,即系统的动能,存在能量损失,这意味着能量不守恒,粒子相互粘附,然后移动。动量保持守恒。初始动能总是大于最终动能。
Types of Colpsion
碰撞主要有两种类型:一种是弹性碰撞,另一种是非弹性碰撞。在第一种情况下,动能是恒定的,而在第二种情况下动能是不守恒的。
Law of Conservation of Linear Momentum
正如我们所知,动量是物体质量和速度的乘积。根据线性动量守恒定律,如果一个物体与另一个物体碰撞,碰撞前物体的总动量等于或等于碰撞后物体的总动能。
设碰撞前的初始速度为$mathrm{u1}$和$mathrm{u2}$。碰撞后的最终速度为$mathrm{v_{1}}$和$mathrm{v_{2}}$。质量是恒定的,因此碰撞后质量保持恒定。力具有相等和相反的反作用力。
$$mathrm{F_1=-F_2}$$
$$mathrm{m_1 a_1=-m_2 a_2}$$
$$mathrm{m_1frac{(v_{1}-u_{1})}{t}=-m_2frac{$$
时间t已取消
$$mathrm{m_1 v_{1}-m_1 u1=-m_2 v_{2}+m_2 u2}$$
$$mathrm{m_1 v_{1}-m_1 u1=m_2 u_{2}-m_2 v_2}$$
$$mathrm{m_1 v_{1}+m_2 v_2=m_2 u_{2}+m_1 u1}$$
或者$$mathrm{m_1 u_{1}+m_2 u_2=m_1 v_{1}+m_2 v_2}$$
因此,碰撞前的总动量等于或等于碰撞后的总动量。
Elastic Colpsion in One Dimension
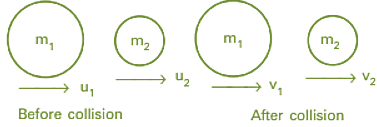
Fig:1 Elastic colpsion in one dimension
假设两个质量为$mathrm{m_1}$和$mathrm{m_2}$的物体或物体以直线或均匀线移动,初始速度为$matherm{u1}}$,$mathr姆{u2}}$($mathrm{u{1}}$大于$mathr姆·{u{2}}$),并且在物体碰撞后,它们的速度变为$mathrem{v_1}$和$mathrm{v_2}$as($mathrem{v_2}$大于$mathrm{v_1}$)
根据动量守恒定律,
$$mathrm{m_1 u_{1}+m_2 u_2=m_1 v_{1}+m_2 v_2}$$
$$mathrm{m_1 u_{1}-m_1 v_1=m_2 v_{2}-m-2 u2}$$
$$mathrm{m_1(u_{1}-v_1)=m_2(v_2-u_2)::…。(1)}$$
根据能量守恒定律,KE是守恒的
$$mathrm{frac{1}{2}m_1u_1^{2}+frac{1}{2}m-1u_2^{2中}=frac{1}}{2}m2v_1^{2}+frac{1}$$
$$mathrm{frac{1}{2}m_1u1^{2}-frac{1}{2}m_1v_1^{2}=frac{1}{2}m_2v_2^{2}-frac{1}$$
$$mathrm{frac{1}{2}m_1(u1 ^{2}-v_1 ^{2中})=frac{1}{2}m_2(v_2 ^{2}-u2 ^{2})}$$
$$mathrm{m_1(u1^{2}-v_1^{2})=m_2(v_2^{2}-u_2^{2*):::…。(2)}$$
将等式(2)除以(1)
$$mathrm{frac{m_1(u1^{2}-v_1^{2})}{m-1(u1-v_1)}=frac{m_2(v_2^{2}-u_2^{2*)}$$
$$mathrm{frac{(u1+v_1)((u1)-v_1)}{(u1)-v_1$$
(由于取消了相同的值)
$$mathrm{(u1+v_1)=(v_2+u2)}$$
$$mathrm{(u1-u_2)=(v_2-v_1)}$$
因此,碰撞前的相对速度$mathrm{(u1-u_2)}$等于碰撞后的相对碰撞$mathrm{(v_2_v_1)}$。
Elastic Colpsion in Two Dimension
从能量守恒的角度来看,
碰撞前保持的总动能(KE)总是与碰撞后保持的总能量(KE)相同或相等。
$$mathrm{frac{1}{2}m_1u_1^{2}+frac{1}{2}m-1u_2^{2中}=frac{1}}{2}m2v_1^{2}+frac{1}$$
(1/2将被取消,所以我们有)
$$mathrm{m_1 u1 ^{2}+m_1 u2 ^{2}=m_2 v_1^{2中}+m_2 v_2^{中}}$$
由于线性动量是恒定的,
碰撞前保持的总线性动量与碰撞后保持的总线动量相同。对于水平组件
$$mathrm{m_1 u_{1}+m_2 u2=m_1 v_{1}:cos heta+m_2 v_2:cos heta}$$
对于垂直组件
$$mathrm{0=m_1 v_{1}sin heta+m_2 v_ 2 sin heta}$$
四个未知量,即$mathrm{m_1,m_2,v_1,u2,heta}$,通过测量四个未知量中的一个,可以求解其他三个未知量的值。
Inelastic Colpsion in One Dimension
在非弹性碰撞中,物体相互粘附,并以与速度相同的方向运动。动量是守恒的,但动能可能会变化,并改变为不同类型的能量。由于物体相互粘连,动量守恒为,
$$mathrm{m_1 u_{1}+m_2 u2=(m_1+m_2)v}$$
在这里,最终速度变为v,我们发现v的值为:
$$mathrm{v=压裂{m_1 u_{1}+m_2 u2}{(m_1+m_2)}}$$
同样损失的动能由,
$$mathrm{KE=frac{1}{2}m_1u_{2}-frac{1}{2}(m_1+m_2)v_2}$$
Inelastic Colpsion in Two Dimension
正如我们所知,任何粒子系统的总线性动量都将保持不变,这意味着总初始动量等于总最终动量。
正如我们所拥有的,
$$mathrm{m_1 u_{1}+m_2 u2=m_1 v_{1}:cos heta+m_2 v_2:cos heta}$$
$$mathrm{0=m_1 v_{1}sin heta-m2 v_ 2 sin heta}$$

Inelastic colpsion in two dimension
当主体彼此粘附时,
$$mathrm{m_1 u_{1}cos heta+m_2 u2=(m_1+m_2)v:cos heta}$$
因此,左边的动量等于右边的线性动量,这是最终的动量。这就是完全非弹性碰撞的方程。碰撞后的速度变得相同。所以最终速度表示为v。
Examples of one and two dimension colpsion
与碰撞有关的一些示例包括:
当你把篮球打在地上时,它会弹回到你身边。在这种情况下,动能保持不变,这意味着这个例子是弹性碰撞。
小粒子和原子之间的碰撞也是弹性碰撞的一个例子。
一个男孩在地上踢足球就是非弹性碰撞的一个例子。
一个扔到墙上的泥球粘在上面,这是非弹性碰撞。
如果两辆车相撞就是非弹性碰撞的一个例子。
如果一个粘土球掉到某个高度,它也会由于非弹性碰撞而粘住。
Conclusion
这个关于碰撞的教程可以看作是线性动量守恒的一个应用。物理学中的各种技术都利用这些概念来了解更多关于碰撞的信息
FAQs
Q1.公交车撞树是哪种类型碰撞的一个例子
在这个例子中,动能(KE)不是恒定的,所以它是非弹性碰撞。
Q2.非弹性碰撞的动能是常数吗
答:不,在非弹性碰撞中,动能(KE)永远不可能是守恒的或恒定的。
Q3.在非弹性碰撞的情况下,动量是恒定的吗
答:是的,在非弹性碰撞中动量是恒定的。
Q4.定义动量守恒
根据动量守恒定律,碰撞之前的动量之和与碰撞之后的总动量之和相同。
问题5.有些物体与其他物体发生碰撞,这是哪种类型的碰撞
Ans.非弹性碰撞
